这是一篇献给我恋人的高等数学教程。为了适应她的基础,我为不少东西做了铺垫。当然,普通读者同样适合这篇文章。在我与她不断学习的过程中,这篇文章也会不断更新。
第一章 函数
1.1 函数是什么
函数是什么呢?对我而言,它像一个“指令清单”,负责把一个东西(数字,或者其它很多事物)变成另一个东西。这就是函数的本质。
我们可以把这个东西叫做 输入(或参数、自变量),而把变换之后的结果叫做 输出(或函数值)。
在数学里,我们常用类似 f(x) 的记号表示函数:
- f:函数名(来自 function)
- x:输入(自变量)
- f(x):函数作用后的结果(函数值)
当然,f 只是一个常用的名字。我们还常用 g、h 等(按字母顺序),甚至 sin、log 这样的名字。
一个例子
还记得这样的式子吗?
$$ 6x^2 - 12x - 18 $$
这类式子通常叫做 表达式。它也可以写成一个函数:
$$ f(x) = 6x^2 - 12x - 18 $$
这意味着:
- 函数名是 f
- 输入是 x
- 函数值是等号右边的表达式结果
通常来说,如果表达式对输入没有特殊限制(比如 $\tfrac{1}{x}$ 限制 $x \neq 0$,因为分母不能为 0),那么 $x$ 就是一个实数。
什么是实数?
实数包含 有理数 和 无理数。
- 有理数:能写成分数形式,分子和分母是整数
- 正数: $7.12 = \tfrac{178}{25}$
- 负数: $-11.03$
- 零: $0$
- 无理数:不能写成分数
- $\pi$、$\sqrt{2}$
与实数相对的是 虚数,它们通常由对负数开平方得到。比如:$\sqrt{-1} = i$
但在初等高数里,我们通常不讨论虚数。
定义域与值域
刚刚我们提到,函数如果对输入没有特殊限制,那么自变量 $x$ 通常是一个实数。那么,如何表示函数的输入可能是哪些值呢?这就是定义域描述的事情。
定义域(Domain)指的就是一个函数所有合法的输入($x$)的集合。换句话说,就是 $x$ 可以是哪些数。
对于我们之前的例子 $f(x) = 6x^2 - 12x - 18$ 来说,它的输入 $x$ 可以是任何实数,因为平方、乘法和减法对任何实数都有效。所以它的定义域是全体实数(我们通常用符号 $\mathbb{R}$ 表示)。
但有些函数就比较“挑剔”了。比如:
- $g(x) = \tfrac{1}{x}$:因为分母不能为 0,所以它的输入 $x$ 就不能是 0。它的定义域就是除 0 以外的所有实数。
- $h(x) = \sqrt{x}$:在实数范围内,我们不能对负数开平方,所以它的输入 $x$ 必须大于或等于 0。它的定义域就是所有非负实数。
既然我们明确了输入(定义域),那么所有可能的输出又会形成一个怎样的集合呢?这就是值域(Range)要告诉我们的。
值域(Range)就是一个函数在它的定义域内,能够产生的所有输出(函数值 $f(x)$)的集合。
我们再来看看刚才的例子:
- $g(x) = \tfrac{1}{x}$:它的输出可以是任何数,但唯独不可能是 0。因为不存在一个数,使得 1 除以它等于 0。所以它的值域是除 0 以外的所有实数。
- $h(x) = \sqrt{x}$:它的输出结果永远不会是负数。所以它的值域是所有非负实数。
- $f(x) = 6x^2 - 12x - 18$:这是一个二次函数。经过一些计算可以知道,它的输出值永远不会低于 -24。所以它的值域是大于或等于 -24 的所有实数。
简单来说:
- 定义域:我们能给函数输入哪些东西?
- 值域:函数能给我们输出哪些东西?
一个函数的定义域和值域是它的重要特征,它们共同描述了函数的“工作范围”。
这个函数做了什么?
回到刚才的函数:
$$ f(x) = 6x^2 - 12x - 18 $$
它的“指令清单”是:
- 输入一个 $x$
- 计算 $x^2$,再乘以 6
- 减去 $12x$
- 再减去 18
- 得到结果 $f(x)$
由此可见:
- 对于同一个输入,输出总是唯一确定的。
- 因为函数的指令清单是固定的,执行多少次都不会变。
这也是函数的重要性质。由此我们可以进一步引出集合与映射的概念(通常也是课本里的定义)。
1.2 函数的参数
形参与实参
在函数中,输入 $x$ 被称为 形式参数(这是计算机科学里的术语,在这里也很有用),简称 形参。它只是一个“代号”,用来在函数的指令清单里引用输入。它可以是任何字母。
注:输入、输出等都是计算机科学的术语。你在数学学习中最好使用 自变量 和 函数值。
在程序设计中,代号甚至常常是一个单词(为了方便阅读和理解代码)。而我的高中数学老师有时喜欢用 t 这个字母。因此,我们也可以把函数写作:
$$ f(t) = 6t^2 - 12t - 18 $$
它与写作 $f(x)$ 完全没有区别。这里的 t 也是 形式参数(形参)。
实际参数(实参)
与 形参 相对应的是 实际参数(实参)。
- 当我们真正使用(计算机科学中叫“调用”)函数时,需要给它一个输入,这个输入就是 实参。
- 例如:我们把数字 3 输入给函数 $f$,就写作:
$$ f(3) $$
这表明:你把 3 作为参数传递给了函数 $f$。 在计算机科学中,这个过程叫做 传参。
举几个例子
1. 实参是一个常数
输入 3:
$$ f(3) = 6 \times 3^2 - 12 \times 3 - 18 = 54 - 36 - 18 = 0 $$
2. 实参是一个变量
实参也可以是一个变量。例如有一个变量 a,我们将它的两倍(2a)作为输入:
$$ \begin{aligned} f(2a) &= 6 \times (2a)^2 - 12 \times (2a) - 18 \\ &= 6 \times 4a^2 - 24a - 18 \\ &= 24a^2 - 24a - 18 \end{aligned} $$
即:
$$ f(2a) = 24a^2 - 24a - 18 $$
这里,我们用 2a(实参) 替换了所有的 x(形参)。
3. 实参是一个更复杂的表达式
如果我们输入 3x+5:
$$ \begin{aligned} f(3x+5) &= 6 \times (3x+5)^2 - 12 \times (3x+5) - 18 \\ &= 6 \times (9x^2 + 30x + 25) - 36x - 60 - 18 \\ &= 54x^2 + 180x + 150 - 36x - 78 \\ &= 54x^2 + 144x + 72 \end{aligned} $$
即:
$$ f(3x+5) = 54x^2 + 144x + 72 $$
这里的 $3x+5$ 是一个 实际参数。 它和定义式 $f(x) = 6x^2 - 12x - 18$ 里的 x(形参) 不一样。
- 定义式里的 x 只是一个代号。
- 而传入的参数(例如 $3x+5$)才是真正的变量或表达式,代表“可能是很多数”的集合。
一个练习
读到这里,我们来看看这样的问题:
如果 $f(x+1) = x^2 - 2x$ 那么 $f(x) = ?$
解答
题目告诉我们:
$$ f(x+1) = x^2 - 2x $$
注意:这里的输入参数是 x+1,而不是单纯的 x。 这意味着,函数的“形参”被替换成了 $x+1$。
要找到 f(x),我们就需要 把 x+1 换回成普通的 x。
步骤 1:做一个代换
令:$t = x + 1$,则我们很容易得到 $x = t - 1$。
因此我们用 $t - 1$ 代换等号右边所有的 $x$,同时函数括号里的 $x+1$ 自然变成了 $t$:
$$ f(t) = (t-1)^2 - 2(t-1) $$
步骤 2:展开化简
$$ \begin{aligned} f(t) &= (t-1)^2 - 2(t-1) \\ &= (t^2 - 2t + 1) - (2t - 2) \\ &= t^2 - 2t + 1 - 2t + 2 \\ &= t^2 - 4t + 3 \end{aligned} $$
步骤 3:还原回 f(x)
因为 $t$ 只是一个代号,所以我们就可以得到 $f(x) = x^2 - 4x + 3$。
1.3 函数图像与方程
我们接下来看看函数的图像,它是帮助我们理解函数的重要工具,对之后对导数与积分的了解也至关重要。我们还是拿 $f(x) = 6x^2 - 12x - 18$ 这个二次函数作为例子:
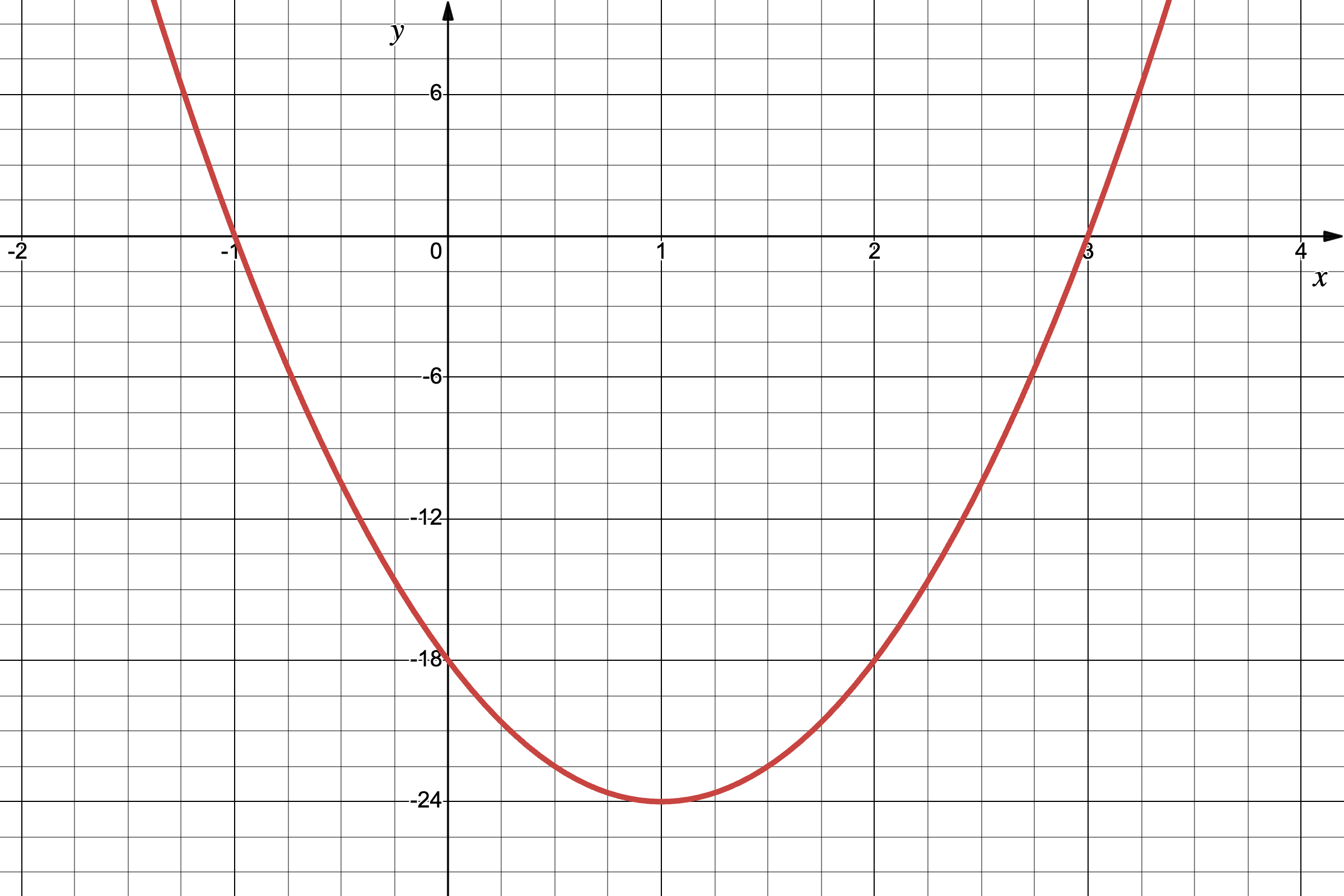
这就是 $f(x) = 6x^2 - 12x - 18$ 的函数图像。我们经常看到 $y = f(x)$ 的表达方式,这种等式的本质是在定义一个名为 $y$ 的变量,它的值是 $f(x)$ 的输出(函数值)。
当我们更改变量 $x$ 的值,函数的输出,即 $f(x)$ 的值会被改变,因此变量 $y$ 的值也会改变。于是我们便把这里的 $x$ 称为 自变量,$y$ 称为 因变量。
注意,这里的 $x$ 与 $y$ 仍然只是代号。如果我们构建 $x = f(y)$,那么 $x$ 就会变成因变量。回到函数图像,我们能观察到一条 抛物线。
二次函数与常数
二次函数的图像都是这样的抛物线,只要函数符合:$f(x) = ax^2 + bx + c \quad (a \neq 0)$ 的形式。
而在我们的例子中,$a = 6$、$b = -12$、$c = -18$。
其中,$a$、$b$、$c$ 被称为 常数,这是因为在同一个函数中,它们的值不会改变。
它们与参数不同:
- 参数的值可能是很多东西,取决于调用时传递的值。
- 常数则是固定不变,是函数“指令清单”的重要组成部分。
如果更改了常数,我们本质上就改变了函数本身。也就是说,我们在构造一个新的函数。
例如令 $c = 0$,我们可以构造 $g(x) = 6x^2 - 12x$;令 $b = 0, c = 0$,得到 $h(x) = 6x^2$,等等。
我们把这三个函数的图像绘制到一起,来观察一下。
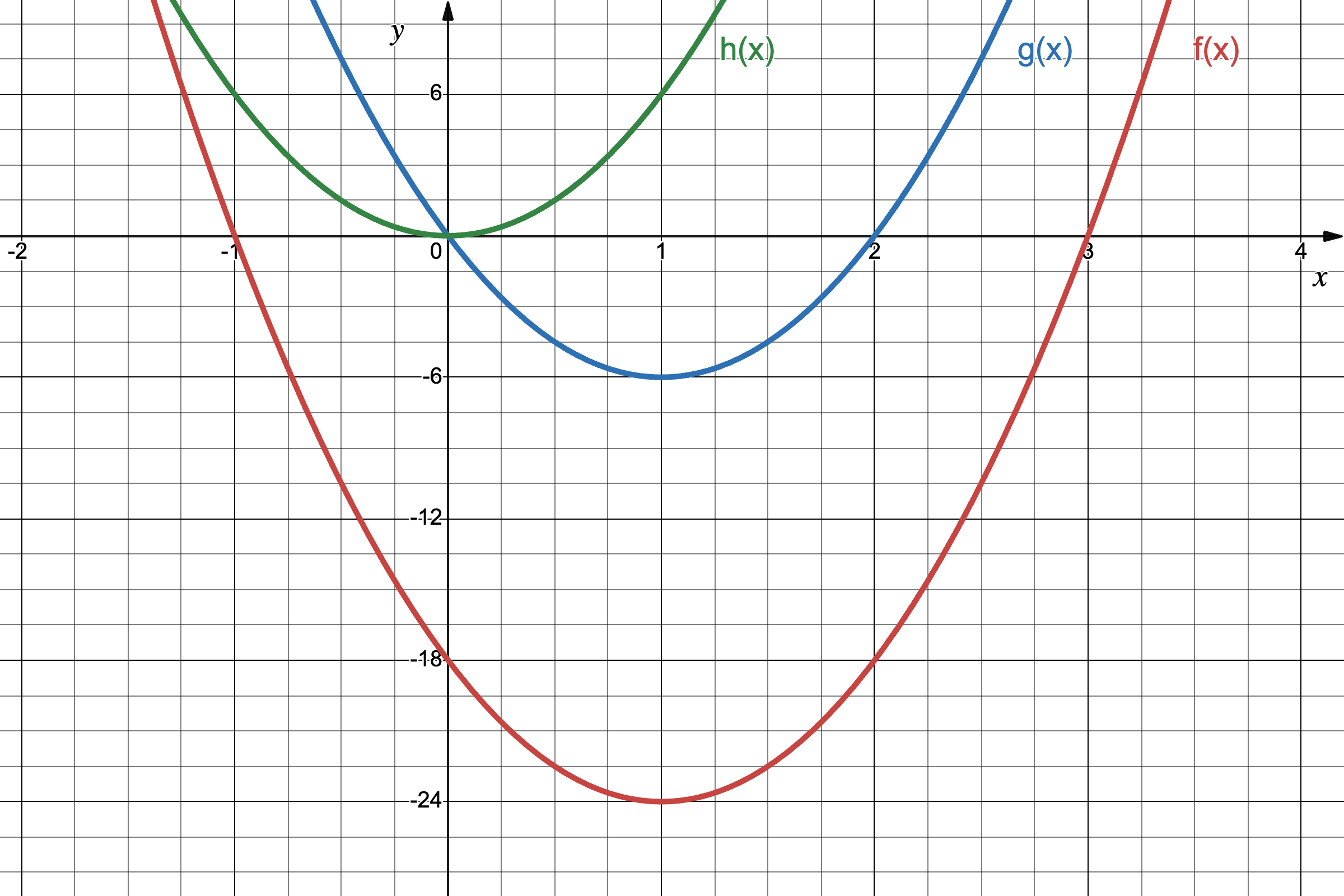
截距
首先来看函数与坐标轴的交点:
- $g(x)$ 与 $h(x)$ 与 $y$ 轴的交点都在点 $(0, 0)$ 处,这意味着当 $x = 0$ 时,$y = 0$。
- 这是因为它们的函数表达式中,$c$ 的值都为 0 —— 也就是说常数项为 0。
我们把一个多项式中不含有未知数的项叫做 常数项。
而 $f(x)$ 与 $y$ 轴交于 $(0, -24)$ 处,这意味着当输入 0 时,$f(x)$ 的输出为 $-24$。 这被称为函数的 纵截距(或 y 截距)。
对应地,函数与 $x$ 轴交点的横坐标称为 横截距,也称为 根 或 零点。也就是说,零点实际上是一个数,而不是一个点。
什么是多项式?
多项式指的是:变量(未知数)与常数(系数)通过加减法、乘法或自然数次的幂这样的运算组合而成的表达式。
例如 $7x^2 + 3x - 5$ 这个多项式中,未知数(变量)是 $x$。$7x^2$ 叫做二次项,其中 7 是二次项的系数。而 $-5$ 则是常数项,它实际上可以写做 $-5x^0$(因为任何数的 0 次方都是 1,而 1 乘以一个数的结果仍是这个数本身)。
对于 $g(x)$ 和 $h(x)$,由于它们的常数项是 0,所以如果输入 $x = 0$,整个式子结果也是 0。
而 $f(x)$ 的情况不同,它与 $y$ 轴交于 $(0, -24)$。
方程与零点
从图像中,我们可以看到,$f(x)$ 的零点为 $x = -1$ 和 $x = 3$。这也是方程$f(x) = 0$,即 $6x^2 - 12x - 18 = 0$ 的根。
方程的本质是一个等式,这可以从它的英文名(equation,等式、方程)中看出。
而方程的根是某一个或几个实数,用它代替方程中的未知数,可以恰好使等式成立。
因为函数的零点就是使函数值为 0 时的自变量,所以当自变量的值等于函数零点时,$f(x) = 0$ 这个等式恰好成立。
于是我们发现:
函数的零点就是方程 $f(x) = 0$ 的根。
到这里,我们已经了解了函数的两个基本性质:截距和零点。接下来我们要看看另外两个重要性质:单调性与奇偶性。
单调性与奇偶性
还记得我们的函数 $f(x) = 6x^2 - 12x - 18$ 的图像吗? 从图像中,你能否看出:随着输入(自变量 $x$)的增大,函数值(输出 $y$)有什么样的增长趋势?
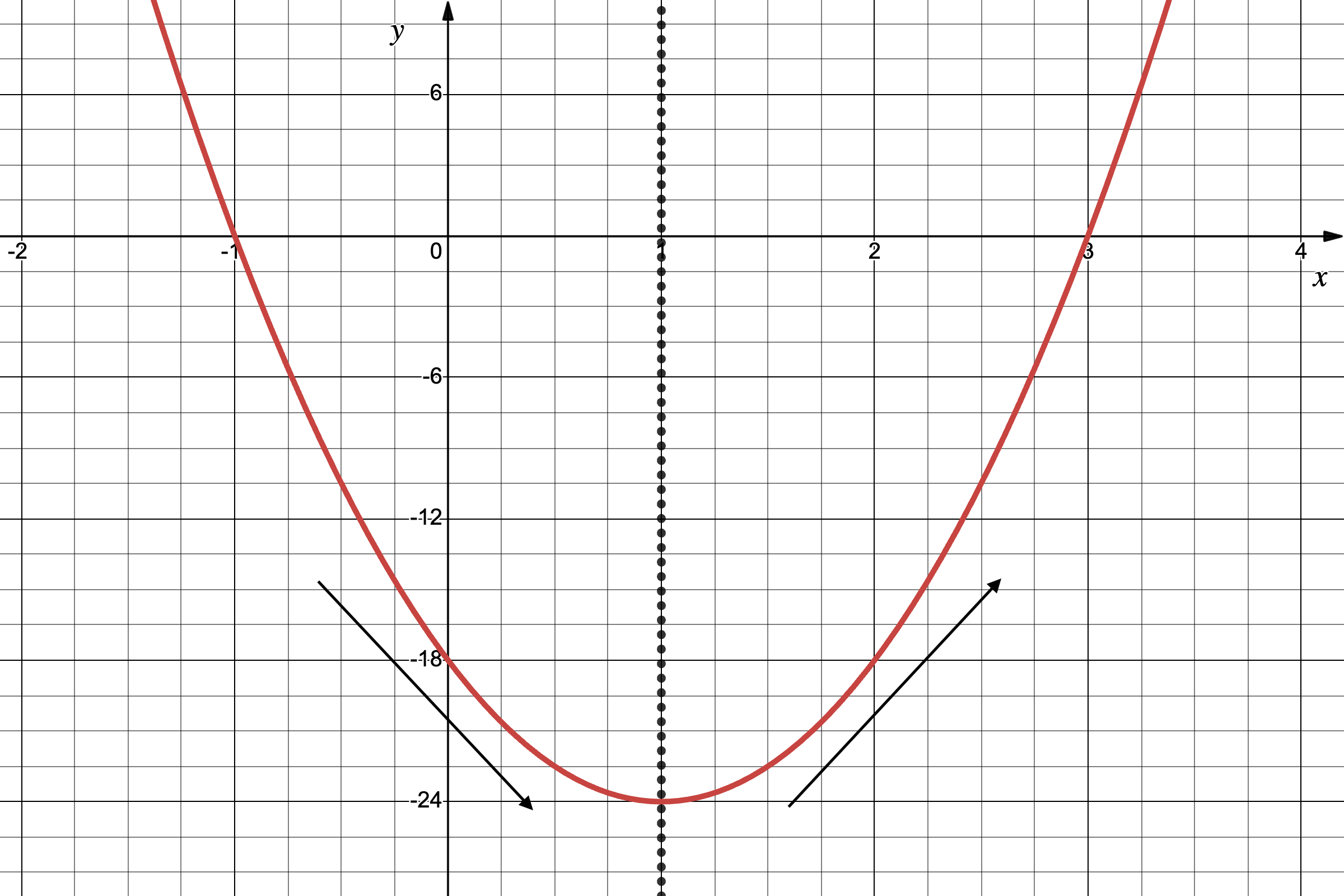
我们可以观察到,图像是关于直线 $x=1$ 对称的(在图中用虚线表示),这条直线被称作图像的对称轴。在对称轴左侧($x<1$),我们能观察到图像呈现下降趋势,而在右侧($x>1$)则是上升趋势。
在数学上,我们称该函数在 $(-\infty,1)$ 区间上单调递减,而在 $(1,+\infty)$ 区间上单调递增。
关于“区间”的概念,请见 1.4 节。
我们也很容易发现,图像在 $x=1$ 处出现了转折。我们叫这个点为函数的极值点。同时,在这个例子中,这个点还是函数的最值点,具体地说,是最小值点。关于极值点和最值点,我们稍后会介绍。
如果函数一直呈现增长或下降的趋势,而没有任何转折,那么我们称这个函数是单调函数。如果一直增长,就是单调递增函数;反之,如果一直下降,则为单调递减函数。
一个小灶:函数单调如何用数学符号语言表达
如果一个函数 $f(x)$ 的定义域是 $I$,那么该函数单调递增可以这么描述:
$$ \forall x_1, x_2 \in I, ; (x_1 < x_2 \implies f(x_1) \leq f(x_2)) $$
是不是看不懂?我们一步步拆解。
首先,从整体上来说,这一串符号描述的是:
随意取两个数 $x_1$ 和 $x_2$,满足:它们都在函数的定义域内,且 $x_1 < x_2$。
那么,如果 $f(x)$ 是单调递增函数,$f(x_1)$ 就一定小于 $f(x_2)$。
更通俗地说:自变量(输入)小,函数值(输出)就一定更小;反正,自变量更大,函数值就一定更大。
而这些符号和我们的描述是怎样对应的呢?我们一个个来看。
首先是 $\forall x_1, x_2 \in I$,这里面 $\forall$ 符号的意思是“对于所有”或者“任意”,而 $\in$ 是“属于”。
也就是说,它代表:“对于所有属于 $I$ 的 $x_1, x_2$”,也就是在函数的定义域内的任意的数 $x_1$ 和 $x_2$。